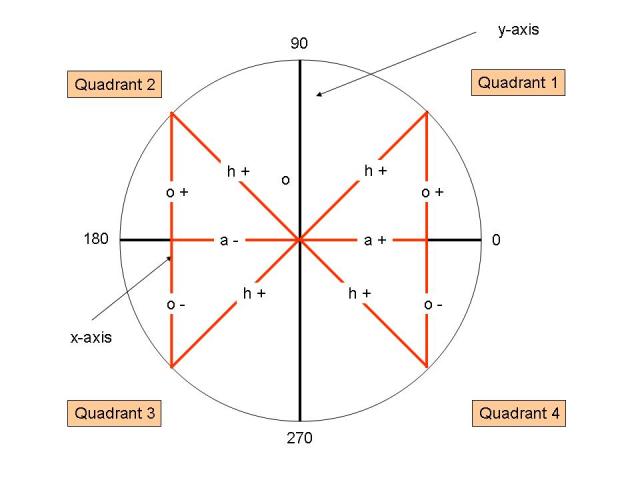
The signs of the trigonometric functions are determined by the quadrant that the angle is in.

If the angle is in the first quadrant, then the sine and cosine and tangent functions are all positive.

If the angle is in the second quadrant, then the sine is positive, the cosine is negative, the tangent is negative.

If the angle is in the third quadrant, then the sine is negative, the cosine is negative, the tangent is positive.

If the angle is in the fourth quadrant, then the sine is negative, the cosine is positive, the tangent is negative.

The hypotenuse is always positive.

The sine is positive in the upper half of the circle because the opposite side is above the x-axis. The sine is negative in the lower half of the circle because the opposite side is below the x-axis.

The cosine is positive in the right half of the circle because the adjacent side is to the right of the y-axis. The cosine is negative in the left half of the circle because the adjacent side is to the left of the y-axis.

The sign of the tangent is determined by the sign of the opposite side and the adjacent side. If one is negative and one is positive, then the sign of the tangent is negative. If both are negative or both are positive, then the sign of the tangent is positive.

The sign of the reciprocal functions of Cosecant, Secant, and Cotangent is determined by the sign of their reciprocals. Cosecant takes from Sine; Secant takes from Cosine; Cotangent takes from Tangent.